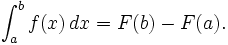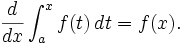History of the Calculus -- Differential and Integral Calculus

Calculus

Calculus is a central branch of mathematics, developed from algebra and geometry, and built on two major complementary ideas.

One concept is differential calculus. It studies rates of change, which are usually illustrated by the slope of a line. Differential calculus is based on the problem of finding the instantaneous rate of change of one quantity relative to another. Examples of typical differential calculus problems are finding the following quantities:

The acceleration and speed of a free-falling body at a particular moment.
The loss in speed and trajectory of a fired projectile, such as an artillery shell or bullet.
Change in profitability over time of a growing business at a particular point.

The other key concept is integral calculus. It studies the accumulation of quantities, such as areas under a curve, linear distance travel, or volume displaced. Integral calculus is the mirror image of differential calculus. Examples of integral calculus problems include finding the following quantities:

The amount of water pumped by a pump with a set power input but varying conditions of pumping losses and pressure.
The amount of money accumulated by a business under varying business conditions.
The amount of parking lot plowed by a snowplow of given power with varying rates of snowfall.

The two concepts, differentiation and integration, define inverse operations in a sense made precise by the fundamental theorem of calculus. In teaching calculus, either concept may be given priority. The usual educational approach is to introduce differential calculus first.

History

Main article: History of calculus

Though the origins of integral calculus are generally regarded as going no farther back than to the ancient Greeks, there is evidence that the ancient Egyptians may have harbored such knowledge as well. (See Moscow Mathematical Papyrus.) Eudoxus is generally credited with the method of exhaustion, which made it possible to compute the area and volume of regions and solids. Archimedes developed this method further, while also inventing heuristic methods which resemble modern day concepts. An Indian Mathematician, Bhaskara (1114-1185), gave an example of what is now called "differential coefficient" and the basic idea of what is now known as "Rolle's theorem". Leibniz and Newton are usually designated the inventors of calculus, mainly for their separate discoveries of the fundamental theorem of calculus and work on notation.

There has been considerable debate about whether Newton or Leibniz was first to come up with the important concepts of the calculus. The truth of the matter will likely never be known. Leibniz' greatest contribution to calculus was his notation; he often spent days trying to come up with the appropriate symbol to represent a mathematical idea. This controversy between Leibniz and Newton was unfortunate in that it divided English-speaking mathematicians from those in Europe for many years, setting back British analysis (i.e. calculus-based mathematics) for a very long time. Newton's terminology and notation was clearly less flexible than that of Leibniz, yet it was retained in British usage until the early 19th century, when the work of the Analytical Society successfully saw the introduction of Leibniz's notation in Great Britain. It is now thought that Newton had discovered several ideas related to calculus earlier than Leibniz had; however, Leibniz was the first to publish. Today, both Leibniz and Newton are considered to have discovered calculus independently.

Lesser credit for the development of calculus is given to Barrow, Descartes, de Fermat, Huygens, and Wallis. A Japanese mathematician, Kowa Seki, lived at the same time as Leibniz and Newton and also elaborated some of the fundamental principles of integral calculus, though this was not known in the West at the time, and he had no contact with Western scholars. [1] (http://www2.gol.com/users/coynerhm/0598rothman.html)

Differential calculus

Main article: Derivative

The derivative measures the sensitivity of one variable to small changes in another variable. A hint is the formula:

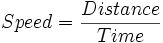$Speed = \frac{Distance}{Time}$ for an object moving at constant speed.

One's speed (a derivative) in a car describes the change in location relative to the change in time. The speed itself may be changing; the calculus deals with this more complex but natural and familiar situation.

Differential calculus determines the instantaneous speed, at any given specific instant in time, not just average speed during an interval of time. The formula Speed = Distance/Time applied to a single instant is the meaningless quotient "zero divided by zero". This is avoided, however, because the quotient Distance/Time is not used for a single instant (as in a still photograph), but for intervals of time that are very short.

The derivative answers the question: as the elapsed time approaches zero, what does the average speed computed by Distance/Time approach? In mathematical language, this is an example of "taking a limit."

More formally, differential calculus defines the instantaneous rate of change (the derivative) of a mathematical function's value, with respect to changes of the variable. The derivative is defined as a limit of a difference quotient.

The derivative of a function gives information about small pieces of its graph. It is directly relevant to finding the maxima and minima of a function — because at those points the graph is flat (i.e. the slope of the graph is zero). Another application of differential calculus is Newton's method, an algorithm to find zeroes of a function by approximating the function by its tangent lines. Differential calculus has been applied to many questions that are not first formulated in the language of calculus.

The derivative lies at the heart of the physical sciences. Newton's law of motion, Force = Mass × Acceleration, has meaning in calculus because acceleration is a derivative. Maxwell's theory of electromagnetism and Einstein's theory of gravity (general relativity) are also expressed in the language of differential calculus, as is the basic theory of electrical circuits and much of engineering.

Integral calculus

Main article: Integral

The definite integral evaluates the cumulative effect of many small changes in a quantity. The simplest instance is the formula

Distance = Speed x Time

for calculating the distance a car moves during a period of time when it is traveling at constant speed. The distance moved is the cumulative effect of the small distances moved in each of the many seconds the car is on the road. The calculus is able to deal with the natural situation in which the car moves with changing speed.

Integral calculus determines the exact distance traveled during an interval of time by creating a series of better and better approximations, called Riemann sums, that approach the exact distance.

More formally, we say that the definite integral of a function on an interval is a limit of Riemann sum approximations.

Applications of integral calculus arise whenever the problem is to compute a number that is in principle (approximately) equal to the sum of the solutions of many, many smaller problems.

The classic geometric application is to area computations. In principle, the area of a region can be approximated by chopping it up into many very tiny squares and adding the areas of those squares. (If the region has a curved boundary, then omitting the squares overlapping the edge does not cause too great an error.) Surface areas and volumes can also be expressed as definite integrals.

Many of the functions that are integrated are rates, such as a speed. An integral of a rate of change of a quantity on an interval of time tells how much that quantity changes during that time period. It makes sense that if one knows their speed at every instant in time for an hour (i.e. they have an equation that relates their speed and time), then they should be able to figure out how far they go during that hour. The definite integral of their speed presents a method for doing so.

Many of the functions that are integrated represent densities. If, for example, the pollution density along a river (tons per mile) is known in relation to the position, then the integral of that density can determine how much pollution there is in the whole length of the river.

Probability, the basis for statistics, provides one of the most important applications of integral calculus.

Foundations

The rigorous foundation of calculus is based on the notions of a function and of a limit; the latter has a theory ultimately depending on that of the real numbers as a continuum. Its tools include techniques associated with elementary algebra, and mathematical induction.

The modern study of the foundations of calculus is known as real analysis. This includes full definitions and proofs of the theorems of calculus. It also provides generalisations such as measure theory and distribution theory.

Fundamental theorem of calculus

The fundamental theorem of calculus states that differentiation and integration are, in a certain sense, inverse operations. More precisely, antiderivatives can be calculated with definite integrals, and vice versa.

This connection allows us to recover the total change in a function over some interval from its instantaneous rate of change, by integrating the latter.

This realization, made by both Newton and Leibniz, was key to the massive proliferation of analytic results after their work became known.

The fundamental theorem provides an algebraic method of computing many definite integrals --without performing limit processes--by finding formulas for antiderivatives. It is also a prototype solution of a differential equation. Differential equations relate an unknown function to its derivatives, and are ubiquitous in the sciences.

1^st Fundamental Theorem of Calculus: If a function f is continuous on the interval [a, b] and F is an antiderivative of f on the interval [a, b], then

$\int_{a}^{b} f(x)\,dx = F(b) - F(a).$

2^nd Fundamental Theorem of Calculus: If f is continuous on an open interval I containing a, then, for every x in the interval,

$\frac{d}{dx}\int_a^x f(t)\, dt = f(x).$

Applications

The development and use of calculus has had wide reaching effects on nearly all areas of modern living. It underlies nearly all of the sciences, especially physics. Virtually all modern developments such as building techniques, aviation, and other technologies make fundamental use of calculus. Many algebraic formulas now used for ballistics, heating and cooling, and other practical sciences were worked out through the use of calculus. In a handbook, an algebraic formula based on calculus methods may be applied without knowing its origins.

The success of calculus has been extended over time to differential equations, vector calculus, calculus of variations, complex analysis, and differential topology.

External links

The Role of Calculus in College Mathematics (http://www.ericdigests.org/pre-9217/calculus.htm)
MathWorld general article on calculus (http://mathworld.wolfram.com/Calculus.html)
Work of Bhaskaracharya II (http://www-groups.dcs.st-and.ac.uk/~history/Projects/Pearce/Chapters/Ch8_5.html)
Online Integrator by Mathematica (http://integrals.wolfram.com/)