Multiplication in Scientific Notation

Scientific Notation is based on powers of the base number 10.

The number 123,000,000,000 in scientific notation is written as : 

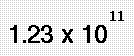
The first number 1.23 is called the coefficient. It must be greater than or equal to 1 and less than 10. 

The second number is called the base . It must always be 10 in scientific notation. The base number 10 is always written in exponent form. In the number 1.23 x 1011 the number 11 is referred to as the exponent or power of ten. 

Rules for Multiplication in Scientific Notation: 

1) Multiply the coefficients 

2) Add the exponents (base 10 remains)

Example 1: (3 x 104)(2x 105) = 6 x 109

What happens if the coefficient is more than 10 when using scientific notation? 

Example 2: (5 x 10 3) (6x 103) = 30. x 106 

While the value is correct it is not correctly written in scientific notation, since the coefficient is not between 1 and 10. We then must move the decimal point over to the left until the coefficient is between 1 and 10. For each place we move the decimal over the exponent will be raised 1 power of ten. 

30.x106 = 3.0 x 107 in scientific notation. 

Example 3: 

(2.2 x 10 4)(7.1x 10 5) = 15.62 x 10 9 = 1.562 x 10 10

Example 4: 

(7 x 104)(5 x 106)(3 x 102) = 105. x 10 12 --now the decimal must be moved two places over and the exponent is raised by 2. Therefore the value in scientific notation is: 1.05 x 10 14

Now Try these:

(write your answers in the form of coefficientx10^exponent) If your answer is 3.5 x 10 ³ you should type 3.5x10^3 in the box then click the submit button).

(2 X 10³)(4X10⁴)=

(6 X 10⁵ )(7 X 10 ⁶)=

(5.5 X 10⁷)(4.2 x 10⁴)=

What happens when the exponent(s) are negative?

We still add the exponents, but use the rules of addition of signed numbers.

Example 5: (3 x 10 ^-3) (3x 10^-3) = 9. x 10^-6

Example 6: (2 x 10 ^-3) (3x 10⁸) = 6. x 10⁵

Now Try these:

(write your answers in the form of coefficientx10^exponent) If your answer is 3.5 x 10 ³ you should type 3.5x10^3 in the box then click the submit button). Multiply the following:

 

(3 X 10^-6)(2X10^-4)=

(5 X 10^-5 )(7 X 10 ¹⁰)=

(5.5 X 10^-7)(4.2 x 10⁴)=

(5 X 10⁷)(8 x 10^-6)(4.2 x 10⁴)=

 

Go to Division in Scientific Notation