An interest rate swap is a derivative in which one party exchanges a stream of interest payments for another party's stream of cash flows. Interest rate swaps can be used by hedgers to manage their fixed or floating assets and liabilities. They can also be used by speculators to replicate unfunded bond exposures to profit from changes in interest rates. As such, interest rate swaps are very popular and highly liquid instruments.

Structure

In an interest rate swap, each counterparty agrees to pay either a fixed or floating rate denominated in a particular currency to the other counterparty. The fixed or floating rate is multiplied by a notional principal amount (say, USD 1 million). This notional amount is generally not exchanged between counterparties, but is used only for calculating the size of cashflows to be exchanged.

The most common interest rate swap is one where one counterparty pays a fixed rate (the swap rate) while receiving a floating rate (usually pegged to LIBOR). Consider the following swap in which Party A agrees to pay Party B periodic interest rate payments of LIBOR + 50 bps (0.50%) in exchange for periodic interest rate payments of 3.00%. Note that there is no exchange of the principal amounts and that the interest rates are on a "notional" (i.e. imaginary) principal amount. Also note that the interest payments are settled in net (e.g. if LIBOR + 50 bps is 1.20% then Party A receives 1.80% and Party B pays 1.80%). The fixed rate (3.00% in this example) is referred to as the swap rate.^[1]

At the point of initiation of the swap, the swap is priced so that it has a net present value of zero. If one party wants to pay 50 bps above the par swap rate, the other party has to pay approximately 50 bps over LIBOR to compensate for this.

Types

Being OTC instruments interest rate swaps can come in a huge number of varieties and can be structured to meet the specific needs of the counterparties. That said, by far the most common are fixed-for-fixed, fixed-for-floating or floating-for-floating. The legs of the swap can be in the same currency or in different currencies. (A single-currency fixed-for-fixed rate swap is generally not possible; since the entire cash-flow stream can be predicted at the outset there would be no reason to maintain a swap contract as the two parties could just settle for the difference between the present values of the two fixed streams, the only exceptions would be where the notional amount on one leg is uncertain or other esoteric uncertainty is introduced)

Fixed-for-floating rate swap, same currency

Party P pays/receives fixed interest in currency A to receive/pay floating rate in currency A indexed to X on a notional N for a tenor T years. For example, you pay fixed 5.32% monthly to receive USD 1M Libor monthly on a notional USD 1 million for 3 years. The party that pays fixed and receives floating coupon rates is said to be long the interest swap.

Fixed-for-floating swaps in same currency are used to convert a fixed rate asset/liability to a floating rate asset/liability or vice versa. For example, if a company has a fixed rate USD 10 million loan at 5.3% paid monthly and a floating rate investment of USD 10 million that returns USD 1M Libor +25 bps monthly, it may enter into a fixed-for-floating swap. In this swap, the company would pay a floating USD 1M Libor+25 bps and receive a 5.5% fixed rate, locking in 20bps profit.

Fixed-for-floating rate swap, different currencies

Party P pays/receives fixed interest in currency A to receive/pay floating rate in currency B indexed to X on a notional N at an initial exchange rate of FX for a tenure of T years. For example, you pay fixed 5.32% on the USD notional 10 million quarterly to receive JPY 3M (JIBOR) monthly on a JPY notional 1.2 billion (at an initial exchange rate of USDJPY 120) for 3 years. For nondeliverable swaps, the USD equivalent of JPY interest will be paid/received (according to the FX rate on the FX fixing date for the interest payment day). No initial exchange of the notional amount occurs unless the Fx fixing date and the swap start date fall in the future.

Fixed-for-floating swaps in different currencies are used to convert a fixed rate asset/liability in one currency to a floating rate asset/liability in a different currency, or vice versa. For example, if a company has a fixed rate USD 10 million loan at 5.3% paid monthly and a floating rate investment of JPY 1.2 billion that returns JPY 1M Libor +50 bps monthly, and wants to lock in the profit in USD as they expect the JPY 1M Libor to go down or USDJPY to go up (JPY depreciate against USD), then they may enter into a Fixed-Floating swap in different currency where the company pays floating JPY 1M Libor+50 bps and receives 5.6% fixed rate, locking in 30bps profit against the interest rate and the fx exposure.

Floating-for-floating rate swap, same currency

Party P pays/receives floating interest in currency A Indexed to X to receive/pay floating rate in currency A indexed to Y on a notional N for a tenor T years. For example, you pay JPY 1M Libor monthly to receive JPY 1M Tibor monthly on a notional JPY 1 billion for 3 years.

Floating-for-floating rate swaps are used to hedge against or speculate on the spread between the two indexes widening or narrowing. For example, if a company has a floating rate loan at JPY 1M Libor and the company has an investment that returns JPY 1M Tibor+30 bps and currently the JPY 1M Tibor = JPY 1M Libor +10bps. At the moment, this company has a net profit of 40 bps. If the company thinks JPY 1M tibor is going to come down or JPY 1M Libor is going to increase in the future and wants to insulate from this risk, they can enter into a Float float swap in same currency where they pay JPY TIBOR +10 bps and receive JPY LIBOR+35 bps. with this, they have effectively locked in a 15 bps profit instead of running with a current 40 bps gain and index risk. The 5bps difference comes from the swap cost which includes the market expectations of the future rates in these two indices and the bid/offer spread which is the swap commission for the swap dealer.

Floating-for-floating rate swaps are also seen where both sides reference the same index, but on different payment dates, or use different business day conventions. These have almost no use for speculation, but can be vital for asset-liability management. An example would be swapping 3M Libor being paid with prior non-business day convention, quarterly on JAJO (i.e. Jan, Apr, Jul, Oct) 30, into FMAN (i.e. Feb, May, Aug, Nov) 28 modified following.

Floating-for-floating rate swap, different currencies

Party P pays/receives floating interest in currency A indexed to X to receive/pay floating rate in currency B indexed to Y on a notional N at an initial exchange rate of FX for a tenor T years. For example, you pay floating USD 1M Libor on the USD notional 10 million quarterly to receive JPY 3M Tibor monthly on a JPY notional 1.2 billion (at an initial exchange rate of USDJPY 120) for 4 years.

To explain the use of this type of swap, consider a US company operating in Japan. To fund their Japanese growth, they need JPY 10 billion. The easiest option for the company is to issue debt in Japan. As the company might be new in the Japanese market without a well known reputation among the Japanese investors, this can be an expensive option. Added on top of this, the company might not have appropriate debt issuance program in Japan and they might lack sophisticated treasury operation in Japan. To overcome the above problems, it can issue USD debt and convert to JPY in the FX market. Although this option solves the first problem, it introduces two new risks to the company:

• FX risk. If this USDJPY spot goes up at the maturity of the debt, then when the company converts the JPY to USD to pay back its matured debt, it receives less USD and suffers a loss.
• USD and JPY interest rate risk. If the JPY rates come down, the return on the investment in Japan might go down and this introduces an interest rate risk component.

The first exposure in the above can be hedged using long dated FX forward contracts but this introduces a new risk where the implied rate from the FX spot and the FX forward is a fixed rate but the JPY investment returns a floating rate. Although there are several alternatives to hedge both the exposures effectively without introducing new risks, the easiest and the most cost effective alternative would be to use a floating-for-floating swap in different currencies. In this, the company raises USD by issuing USD Debt and swaps it to JPY. It receives USD floating rate (so matching the interest payments on the USD Debt) and pays JPY floating rate matching the returns on the JPY investment.

Fixed-for-fixed rate swap, different currencies

Party P pays/receives fixed interest in currency A to receive/pay fixed rate in currency B for a term of T years. For example, you pay JPY 1.6% on a JPY notional of 1.2 billion and receive USD 5.36% on the USD equivalent notional of 10 million at an initial exchange rate of USDJPY 120.

Other variations

A number of other variations are possible, although far less common. Mostly tweaks are made to ensure that a bond is hedged "perfectly", so that all the interest payments received are exactly offset by the swap. This can lead to swaps where principal is paid on one or more legs, rather than just interest (for example to hedge a coupon strip), or where the balance of the swap is automatically adjusted to match that of a prepaying bond (such as RMBS).

Uses

Interest rate swaps were originally created to allow multi-national companies to evade exchange controls. Today, interest rate swaps are used to hedge against or speculate on changes in interest rates.

Hedging

Today, interest rate swaps are often used by firms to alter their exposure to interest-rate fluctuations, by swapping fixed-rate obligations for floating rate obligations, or vice versa. By swapping interest rates, a firm is able to alter its interest rate exposures and bring them in line with management's appetite for interest rate risk. For example, Fannie Mae uses interest rate derivatives to hedge its cash flows. The products it uses are pay-fixed swaps, receive-fixed swaps, basis swaps, interest rate cap and swaptions, and forward starting swaps. Its "cash flow hedges" had a notional value of $872 billion at December 31, 2003, while its "fair value hedges" stood at $169 billion (SEC Filings) (2003 10-K page 79). Its "net value" on "a net present value basis, to settle at current market rates all outstanding derivative contracts" was (7,712) million and 8,139 million, which makes a total of 6,633 million when a "purchased options time value" of 8,139 million is added.

What Fannie Mae doesn't want is for example a wide "duration gap" for a long period. If rates turn the opposite way on a duration gap the cash flow from assets and liabilities may not match, resulting in inability to pay the bills on liabilities. It reports the duration gap regularly in its (8-K Regulation FD Disclosure), see earlier 10-K's for charts and more information (Investor Relations: Annual Reports & Proxy Statements). (Dec 1999 - Dec 2002 duration gap), (2003 gap).

Speculation

Interest rate swaps are also used speculatively by hedge funds or other investors who expect a change in interest rates or the relationships between them. Traditionally, fixed income investors who expected rates to fall would purchase cash bonds, whose value increased as rates fell. Today, investors with a similar view could enter a floating-for-fixed interest rate swap; as rates fall, investors would pay a lower floating rate in exchange for the same fixed rate.

Interest rate swaps are also very popular due to the arbitrage opportunities they provide. Due to varying levels of creditworthiness in companies, there is often a positive quality spread differential which allows both parties to benefit from an interest rate swap.

The interest rate swap market is closely linked to the Eurodollar futures market which trades at the Chicago Mercantile Exchange.

Valuation and pricing

The present value of a plain vanilla (i.e. fixed rate for floating rate) swap can easily be computed using standard methods of determining the present value (PV) of the fixed leg and the floating leg.

The value of the fixed leg is given by the present value of the fixed coupon payments known at the start of the swap, i.e.

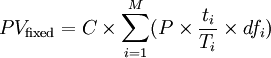
where C is the swap rate, M is the number of fixed payments, P is the notional amount, t_i is the number of days in period i, T_i is the basis according to the day count convention and df_i is the discount factor.

Similarly, the value of the floating leg is given by the present value of the floating coupon payments determined at the agreed dates of each payment. However, at the start of the swap, only the actual payment rates of the fixed leg are known in the future, whereas the forward rates (derived from the yield curve) are used to approximate the floating rates. Each variable rate payment is calculated based on the forward rate for each respective payment date. Using these interest rates leads to a series of cash flows. Each cash flow is discounted by the zero-coupon rate for the date of the payment; this is also sourced from the yield curve data available from the market. Zero-coupon rates are used because these rates are for bonds which pay only one cash flow. The interest rate swap is therefore treated like a series of zero-coupon bonds. Thus, the value of the floating leg is given by the following:

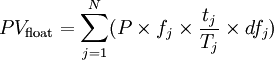
where N is the number of floating payments, f_j is the forward rate, P is the notional amount, t_j is the number of days in period j, T_j is the basis according to the day count convention and df_j is the discount factor. The discount factor always starts with 1. The discount factor is found as follows:

[Discount factor in the previous period]/[1 + (Forward rate of the floating underlying asset in the previous period × Number of days in period/360)].

The fixed rate offered in the swap is the rate which values the fixed rates payments at the same PV as the variable rate payments using today's forward rates, i.e.:

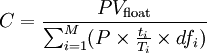^[2]

Therefore, at the time the contract is entered into, there is no advantage to either party, i.e.,

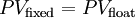
Thus, the swap requires no upfront payment from either party.

During the life of the swap, the same valuation technique is used, but since, over time, the forward rates change, the PV of the variable-rate part of the swap will deviate from the unchangeable fixed-rate side of the swap. Therefore, the swap will be an asset to one party and a liability to the other. The way these changes in value are reported is the subject of IAS 39 for jurisdictions following IFRS, and FAS 133 for U.S. GAAP. Swaps are marked to market by debt security traders to visualize their inventory at a certain time.

Risks

Interest rate swaps expose users to interest rate risk and credit risk.

• Interest rate risk originates from changes in the floating rate. In a plain vanilla fixed-for-floating swap, the party who pays the floating rate benefits when rates fall. (Note that the party that pays floating has an interest rate exposure analogous to a long bond position.)

• Credit risk on the swap comes into play if the swap is in the money or not. If one of the parties is in the money, then that party faces credit risk of possible default by another party. This is true for all swaps where there is no exchange of principal.

Market size

The Bank for International Settlements reports that interest rate swaps are the largest component of the global OTC derivative market. The notional amount outstanding as of December 2006 in OTC interest rate swaps was $229.8 trillion, up $60.7 trillion (35.9%) from December 2005. These contracts account for 55.4% of the entire $415 trillion OTC derivative market. However, interest rate swaps are not standardized enough to allow them to be traded through a futures exchange like an option or a futures contract.

References

1. "Interest Rate Swap" by Fiona Maclachlan, The Wolfram Demonstrations Project.
2. Understanding interest rate swap math & pricing. California Debt and Investment Advisory Commission (2007-01). Retrieved on 2007-09-27.

• Pricing and Hedging Swaps, Miron P. & Swannell P., Euromoney books 1991

External links

• Bank for International Settlements - Semiannual OTC derivatives statistics
• Investopedia - Spreadlock - An interest rate swap future (not an option)
• Basic Fixed Income Derivative Hedging - Article on Financial-edu.com.