| When
the graphic box is clicked on a three dimensional grid will appear. You will not
be able to see the z-axis because it is coming out at you. Go to view 2 and the
axis will be rotated so you may view the grid in 3-Dimensions. Click on any point
and notice the lower left hand corner; a set of three coordinates appear (x,y,z).
What
do you think the z now represents?
To get a better feel for 3-D geometry click on cube at the right side of the menu
box. Click on "label cube" , the letters A,B,C,D will appear. **What
are the x,y,z coordinates for A______ B______ C_____ D____
**What is the measure
of line segment AB? _____ When
you have completed click off the cube and label cube
| | | To
rotate object hold left mouse button down and slide cursor arrow over object |
In tutorial II you
used Kinemage to measure angles and distances in two dimensions. Because the real
world is 3- Dimensions, lets take a look at measuring angles and distances in
3-D space. When measuring angles in space we will need to click four consecutive
points. Can you explain why three point will not be enough?
(Optional: In solid geometry the dihedral angle is defined as he angle formed
by the intersection of two planes. A dihedral angle may be regarded as formed
by the rotation of a plane about any line in the plane of an axis. Thus the value
of a dihedral angle depends upon the amount of rotation about the edge, and not
really upon the extent of the planes.)
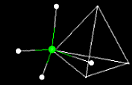
Click on two planes, and "label plane". Go to measure under the Other
pulldown. Just as you measured angles in Tutorial II, click point A, then B, then
point C. This will give you the measure of <ABC. Now click on point D you will
have measured the dihedral angle ABCD (see dhr= on the lower right of the black
Mage box. Much
like angles shown in tutorial 2 required three points located on a two dimensional
plane, the dihedral angles demonstrated here requires four points in three dimensional
space. **What
is the measure of <ABC?_____
**What is the measure of the dihedral angle
ABCD formed by the intersection of the two planes?______
Clear the screen of the planes and labels. Return to View 2. Choose dihedral 1,
click on label angle. Click consecutively points A,B,C.D notice the lower right
gives the angle between the last three points and that dhr= gives the dihedral
angle for ABCD.
Go back to View 1, it shows the dihedral angle face on. Measure the angle as you
see it, face on. What is this telling you? Rotate the image about several axis
to gain a better understanding of a dihedral angle.
Clear the screen of dihedral angle 1. Repeat using the other sample dihedral angles
(no letters will appear). Try to rotate the axis until you gain a clear understanding
of dihedral angles. You may also use this module to form three dimensional images.
These images may be saved and used on your own databases. (To save images will
require the use of text editor, so check with your teacher first).
Activities for Students:
1) In tutorial II we used the Pythagorean theorem to find the diagonal of a square
(a^2+b^2=c^2), and then checked the results using Kinemage. What equation would
represent the diagonal of a cube? Why? Test out your theory and them use Kinemage
to check you reasoning.
2)Try creating several 3-Dimensional figures using the 3-D grid. It may be helpful
to be in either view2 or view3 when this is done.
|