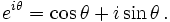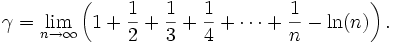Leonhard Euler

Leonhard Euler (1707-1783)

Leonhard Euler(April 15, 1707 â€“ September 18, 1783) was a Swiss mathematician and physicist. He is considered to be one of the greatest mathematicians of all time. Euler was the first to use the term "function" to describe an expression involving various arguments; i.e., y = f(x). Also he introduced lasting notation for common geometric functions such as sine, cosine, and tangent.

Born and educated in Basel, he showed an early talent for mathematics and languages. He worked as a professor of mathematics in St. Petersburg and later in Berlin. He was the most prolific mathematicin of them all, his collected work filling over 70 volumes. He dominated the 18th century mathematics and deduced many consequences of the newly invented calculus. He was almost completely blind for the last seventeen years of his life, during which time he produced almost half of his writings.

Biography

Leonhard Euler was born in Basel, Switzerland, but was raised on the town of Riehen (near Basel) by his mother Margret Brucker and father Paul Euler, a Lutheran minister. Although in his childhood he exhibited great mathematical talents, his father wanted him to study theology. In 1720 Euler began his studies at the University of Basel. There he met the Bernoulli brothers, Daniel and Nikolaus, who noticed Euler's skills in mathematics. Euler's father had attended Jakob Bernoulli's mathematical lectures and when Daniel and Nikolaus asked him to allow his son to study mathematics, he finally agreed.

In 1727 Euler was invited to St. Petersburg by Catherine I of Russia where he became a professor of physics and mathematics. Euler was the first to publish a systematic introduction to mechanics in Mechanica sive motus scientia analytice exposita (1736, Mechanics or motion explained with analytical science â€”that is, calculus). While in Russia, Euler participated in an extensive astronomical project by the Russian Academy of Sciences on the passage of Venus over the Sun. During this time he had to become a Cossack to ensure safe passage of scientific equipment and collaboration of local authorities.

In 1733 he married Katharina Gsell, the daughter of the director of the academy of arts. They had thirteen children, of whom only three sons and two daughters survived. The descendants of his children occupied prominent positions in the 19th century Russia.

In 1735 he lost much of his vision due to his observation of the sun without filtering-out the excessive radiation. Despite this handicap, Euler continued to be productive, perhaps due to his extraordinary powers of memory and mental calculation. It is reported that once he let his assistant calculate a series to 17 summands and noticed an error in the 50th digit.

In 1741 Euler accepted a position at the Academy of Sciences in Berlin, however, due to various reasons, among which was the lack of the king's support, he returned to St. Petersburg in 1766, where he remained for the rest of his life.

It has been estimated that it would take eight hours of work per day for 50 years to copy all his works by hand. It was not until 1910 that a complete collection of his works was published. It was told by Legendre that often he would write down a complete mathematical proof between the first and the second call for supper.

Euler was a deeply religious Calvinist throughout his life, however the frequently quoted remark

"Sir, (a+bⁿ)/n = x, hence God exists; reply!"

with which Euler reportedly challenged Denis Diderot at the court of Catherine the Great is likely not true. When Euler died, the mathematician and philosopher Marquis de Condorcet commented,

"...il cessa de calculer et de vivre,"

he ceased to calculate and ceased to live.

Discoveries

Euler, with Daniel Bernoulli, developed the Euler-Bernoulli beam equation that allows the calculation of stress in beams. Euler also deduced the Euler equations, a set of laws of motion in fluid dynamics, formally identical to the Navier-Stokes equations, explaining, among other phenomena, propagation of the shock waves.

Euler discovered quadratic reciprocity and proved that all even perfect numbers must be of Euclid's form. He investigated primitive roots, found new large primes, and deduced the infinitude of the primes from the divergence of the harmonic series. This was the first breakthrough in this area in two thousand years, heralding the birth of the analytic number theory. His work on factoring whole numbers over the complexes marked the beginning of the algebraic number theory.

Amicable numbers had been known for two thousand years before Euler, and in all that time only 3 pairs were discovered. Euler found 59 more.

Leonhard Euler:

Elaborated the theory of higher transcendental functions by introducing the gamma function and the gamma density functions.

Introduced a new method for solving 4th degree polynomials.

Proved Newton's identities, Fermat's little theorem, Fermat's theorem on sums of two squares, and made distinct contributions to the Lagrange's four-square theorem.

Made contributions to combinatorics, the calculus of variations and difference equations.

Created the theory of hypergeometric series, q-series and the analytic theory of continued fractions.

Solved a multitude of diophantine equations. Discovered the hyperbolic geometric functions.

Calculated integrals with complex limits, which led (via Cauchy) to contour integration and complex analysis.

Discovered the addition theorem for elliptic integrals.

Invented the calculus of variations, including its most well-known result, the Euler-Lagrange equation.

Proved the binomial theorem for binomials with real number exponents.

Described numerous applications of Bernoulli's numbers, Fourier series, Venn diagrams, Euler's numbers, e and pi constants, continued fractions and integrals.

Discovered the infinite product and partial fraction representations of the trigonometric functions.

Explicated logarithms of negative numbers.

Integrated Leibniz's differential calculus with Newton's method of fluxions. Pioneered applications of calculus to physics.

Co-discovered the Euler-Maclaurin formula which facilitates calculation of integrals, sums, and series.

Published substantial contributions to the theory of differential equations.

Defined a series of approximations which are used in computational mechanics. The most useful of these approximations is known as the Euler's method.

Created the Latin square, which likely inspired Howard Garns' number puzzle SuDoku.

In number theory, Euler invented the totient function. The totient Ï†(n) of a positive integer n is defined to be the number of positive integers less than or equal to n and coprime to n. For example, Ï†(8) = 4 since the four numbers 1, 3, 5 and 7 are coprime to 8. With this function Euler was able to generalize Fermat's little theorem.

In 1735, Euler reaffirmed his scientific reputation by solving the long-standing Basel problem:

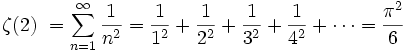$\zeta(2) \ = \sum_{n=1}^\infty \frac{1}{n^2} = \frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} + \cdots = \frac{\pi^2}{6}$ ,

where $Î¶(s)$ is the Riemann zeta function and also described how to evaluate the zeta function at any positive even number.

Euler also showed the usefulness, consistency, and simplicity of defining the exponent of an imaginary number by means of the Euler's formula

$e^{i \theta} = \cos\theta + i\sin\theta \,.$

which establishes the central role of the exponential function in elementary analysis, where virtually all functions are either variations of the exponential function or polynomials. This formula was called "the most remarkable formula in mathematics" by Richard Feynman (Lectures on Physics, p.I-22-10).

Euler's identity is a special case of this

$e^{i \pi} +1 = 0 \,.$

In 1735, Euler defined the Euler-Mascheroni constant useful for solution of differential equations:

$\gamma = \lim_{n \rightarrow \infty } \left( 1+ \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \cdots + \frac{1}{n} - \ln(n) \right).$

In geometry and algebraic topology, there is a relationship (also called the Euler's Formula) which relates the number of edges, vertices, and faces of a simply connected polyhedron. Given such a polyhedron, the sum of the vertices and the faces is always the number of edges plus two. i.e.: F - E + V = 2. The theorem also applies to any planar graph. For nonplanar graphs, there is a generalization: If the graph can be embedded in a manifold M, then F - E + V = Ï‡(M), where Ï‡ is the Euler characteristic of the manifold, a constant which is invariant under continuous deformations. The Euler characteristic of a simply-connected manifold such as a sphere or a plane is 2. A generalization of Euler's formula for arbitrary planar graphs exists: F - E + V - C = 1, where C is the number of components in the graph.

In 1736 Euler solved, or rather proved insoluble, a problem known as the seven bridges of KÃ¶nigsberg, publishing a paper Solutio problematis ad geometriam situs pertinentis which was the earliest application of graph theory or topology.

In 1739 Euler wrote Tentamen novae theoriae musicae, which was an attempt to combine mathematics and music; commented upon that "for musicians it was too advanced in its mathematics and for mathematicians it was too musical."

Distinctions

The asteroid 2002 Euler is named in his honor.

Euler was ranked number 77 on Michael H. Hart's list of the most influential figures in history.

For nearly two decades (1979 to 1996), Euler was featured on a Swiss banknote. http://mypage.bluewin.ch/a-z/jke/CH-Noten/bn01090.htm

External links

John J. O'Connor and Edmund F. Robertson. Leonhard Euler at the MacTutor archive.
Euler Archive
Biography of Leonhard Euler

	_ ________________ ____EDinformatics Home

Leonhard Euler

Biography

Discoveries

Distinctions

Further reading

External links